The Pierce expansion, or alternated Egyptian product, of a real number 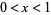 is the unique increasing sequence {a_1,a_2,...}" src="https://mathworld.wolfram.com/images/equations/PierceExpansion/Inline2.gif" style="height:15px; width:66px" /> of positive integers 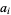 such that

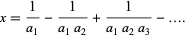(1)

A number 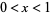 has a finite Pierce expansion iff  is rational.

Special cases are summarized in the following table.

	OEIS	Pierce expansion
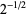	A091831	1, 3, 8, 33, 35, 39201, 39203, 60245508192801, ...
Catalan's constant	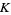A132201	1, 11, 13, 59, 582, 12285, 127893, 654577, ...
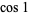	A118239	1, 2, 12, 30, 56, 90, 132, 182, 240, ...
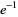	A020725	2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...
Euler-Mascheroni constant	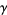A006284	1, 2, 6, 13, 21, 24, 225, 615, 17450, ...
natural logarithm of 2	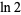A091846	1, 3, 12, 21, 51, 57, 73, 85, 96, ...
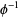	A118242	1, 2, 4, 17, 19, 5777, 5779, 192900153617, ...
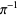	A006283	3, 22, 118, 383, 571, 635, 70529, ...
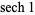		1, 2, 3, 8, 9, 24, 37, 85, ...
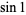	A068377	1, 6, 20, 42, 72, 110, 156, 210, 272, ...

If  is of the form

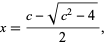(2)

then there is a closed-form for the Pierce expansion given by

{c_0-1,c_0+1,c_1-1,c_1+1,c_2-1,c_2+1,...}, " src="https://mathworld.wolfram.com/images/equations/PierceExpansion/NumberedEquation3.gif" style="height:15px; width:304px" />

(3)

where

			(4)
			(5)

and 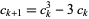 (Shallit 1984). This recurrence has explicit solution

(6)

not noted by Shallit (1984).

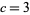, corresponding to 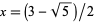, has the particularly beautiful form

			(7)
			(8)

where 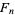 is a Fibonacci number.

The following table gives coefficients 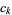 and 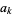 for some small integer .

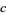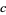		OEIS	{c_k}" src="https://mathworld.wolfram.com/images/equations/PierceExpansion/Inline39.gif" style="height:15px; width:22px" />	OEIS	{a_k}" src="https://mathworld.wolfram.com/images/equations/PierceExpansion/Inline40.gif" style="height:15px; width:23px" />
3		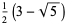A001999	3, 18, 5778, 192900153618, ...	A006276	2, 4, 17, 19, 5777, 5779, ...
4		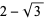	4, 52, 140452, 2770663499604052, ...		3, 5, 51, 53, 140451, 140453, ...
5		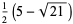	5, 110, 1330670, 2356194280407770990, ...		4, 6, 109, 111, 1330669, 1330671, ...
6		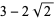A112845	6, 198, 7761798, 467613464999866416198, ...	A006275	5, 5, 7, 197, 199, 7761797, ...

REFERENCES:

Erdős, P. and Shallit, J. O. "New Bounds on the Length of Finite Pierce and Engel Series." Sem. Theor. Nombres Bordeaux 3, 43-53, 1991.

Keselj, V. "Length of Finite Pierce Series: Theoretical Analysis and Numerical Computations." Sep. 10, 1996. https://www.cs.uwaterloo.ca/research/tr/1996/21/cs-96-21.pdf.

Mays, M. E. "Iterating the Division Algorithm." Fib. Quart. 25, 204-213, 1987.

Pierce, T. A. "On an Algorithm and Its Use in Approximating Roots of Polynomials." Amer. Math. Monthly 36, 523-525, 1929.

Salzer, H. E. "The Approximation of Numbers as Sums of Reciprocals." Amer. Math. Monthly 54, 135-142, 1947.

Shallit, J. O. "Some Predictable Pierce Expansions." Fib. Quart. 22, 332-335, 1984.

Shallit, J. O. "Metric Theory of Pierce Expansions." Fib. Quart. 24, 22-40, 1986.

Sloane, N. J. A. Sequences A001999/M3055, A006275/M1342, A006283/M3092, A006284/M1593, A006276/M1298, A020725, A091831, A091846, A112845, A118242, and A132201 in "The On-Line Encyclopedia of Integer Sequences."