A sultan has granted a commoner a chance to marry one of his 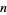 daughters. The commoner will be presented with the daughters one at a time and, when each daughter is presented, the commoner will be told the daughter's dowry (which is fixed in advance). Upon being presented with a daughter, the commoner must immediately decide whether to accept or reject her (he is not allowed to return to a previously rejected daughter). However, the sultan will allow the marriage to take place only if the commoner picks the daughter with the overall highest dowry. Then what is the commoner's best strategy, assuming he knows nothing about the distribution of dowries (Mosteller 1987)?

Since the commoner knows nothing about the distribution of the dowries, the best strategy is to wait until a certain number  of daughters have been presented, then pick the highest dowry thereafter (Havil 2003, p. 134). The exact number to skip is determined by the condition that the odds that the highest dowry has already been seen is just greater than the odds that it remains to be seen and that if it is seen it will be picked. This amounts to finding the smallest  such that

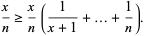(1)

More specifically, the probability of obtaining the maximum dowry after waiting for  out of 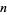 daughters is

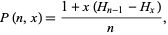(2)

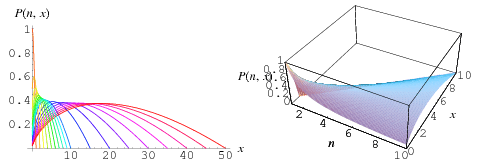
where 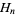 is a harmonic number (Havil 2003, p. 137), plotted above for a number of specific values of  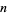as a function of  (left figure above) and as a surface plot in 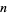 and  (right figure).

The solution is therefore the smallest  such that

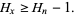(3)

Solving,

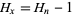(4)

numerically and taking the ceiling function  then gives the solutions 0, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, ... (OEIS A054404) for 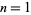, 2, ... daughters.

Surprisingly, the convergents for the continued fraction of 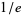, given by 0, 1/2, 1/3, 3/8, 4/11, 7/19, 32/87, 39/106, 71/193, 465/1264, ... (OEIS A007676 and A007677), correspond exactly to pairs 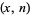, where  is the optimal value for 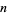 daughters (Havil 2003, p. 137).

An approximate solution can be obtained by using a series expansion for 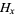 about infinity,

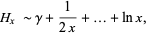(5)

where 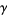 is the Euler-Mascheroni constant, and plugging this approximation into (4), giving

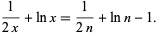(6)

This can be solved in closed form to give an approximate solution to ,

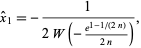(7)

where 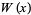 is the Lambert W-function. In fact, taking  gives the correct result for .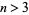

Another approximation can be obtained by taking a series expansion of 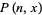 to obtain

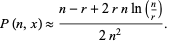(8)

Taking the derivative and setting equal to 0 then gives

(9)

which is within 1 of the correct answer for all .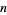

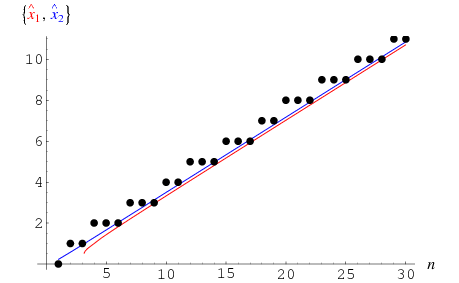
The plot above illustrates these two approximations (red and blue curves) together with the actual values (black dots). Both approximations have series expansions of the form

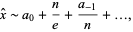(10)

where 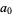 and 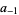 are small constants.

The problem is most commonly stated with 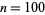 daughters, which gives the result that the commoner should wait until he has seen 37 of the daughters, then pick the first daughter with a dowry that is bigger than any preceding one. With this strategy, his odds of choosing the daughter with the highest dowry are surprisingly high: about  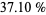(Honsberger 1979, pp. 104-110, Mosteller 1987; Havil 2003, p. 136). As the number of daughters increases, this tends towards  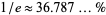(OEIS A068985).

REFERENCES:

Havil, J. "Optimal Choice." §13.13 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 34-138, 2003.

Honsberger, R. "Some Surprises in Probability." Ch. 5 in Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., pp. 104-110, 1979.

Mosteller, F. "Choosing the Largest Dowry." Problem 47 in Fifty Challenging Problems in Probability with Solutions. New York: Dover, pp. 73-77, 1987.

Sloane, N. J. A. Sequences A007676/M0869, A007677/M2343, A054404 and A068985 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم صناعة الشبابيك يشرع بإدامة شباكين قديمين لمرقد الإمامين العسكريين (عليهما السلام)

فرقة العباس (عليه السلام) تختتم خدماتها المقدمة للزائرين في سامراء

موكب العتبتين المقدستين يحيي ذكرى استشهاد الإمام الهادي (عليه السلام) في سامراء

العتبة العسكرية المقدسة تكرّم وفد العتبة العباسية المقدسة لمشاركته في تقديم الخدمات للزائرين

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد