Define the sequence 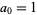, , 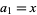and

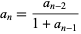(1)

for 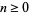. The first few values are

			(2)
			(3)
			(4)
			(5)

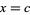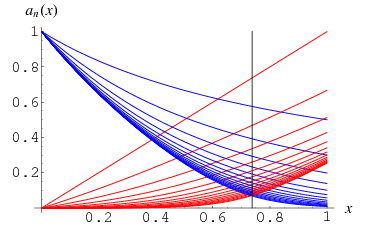
Janssen and Tjaden (1987) showed that this sequence converges for exactly one value , where 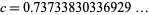 (OEIS A085835), confirming Grossman's conjecture. However, no analytic form is known for this constant, either as the root of a function or as a combination of other constants. The plot above shows the first few iterations of  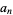for 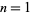 to 30, with odd  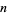shown in red and even  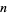shown in blue, for  ranging from 0 to 1. As can be seen, the solutions alternate by parity. For each fixed 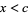, the red values go to 0, while the blue values go to some positive number.

Nyerges (2000) has generalized the recurrence to the functional equation

(6)

REFERENCES:

Ewing, J. and Foias, C. "An Interesting Serendipitous Real Number." In Finite versus Infinite: Contributions to an Eternal Dilemma (Ed. C. Caluse and G. Păun). London: Springer-Verlag, pp. 119-126, 2000.

Finch, S. R. "Grossman's Constant." §6.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 429-430, 2003.

Grossman, J. W. "Problem 86-2." Math. Intel. 8, 31, 1986.

Janssen, A. J. E. M. and Tjaden, D. L. A. Solution to Problem 86-2. Math. Intel. 9, 40-43, 1987.

Michon, G. P. "Final Answers: Numerical Constants." http://home.att.net/~numericana/answer/constants.htm#grossman.

Nyerges, G. "The Solution of the Functional Equation 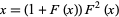." Preprint, Oct. 19, 2000. http://eent3.sbu.ac.uk/Staff/nyergeg/www/etc/fneq.pdf.

Sloane, N. J. A. Sequence A085835 in "The On-Line Encyclopedia of Integer Sequences."