Let

(1)

(OEIS A064853) be the arc length of a lemniscate with 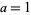. Then the lemniscate constant is the quantity

			(2)
			(3)
			(4)
			(5)
			(6)

(OEIS A062539; Abramowitz and Stegun 1972; Finch 2003, p. 420), where 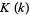 is a complete elliptic integral of the first kind. Todd (1975) cites T. Schneider as proving  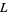to be a transcendental number in 1937.

The quantity

			(7)
			(8)

(OEIS A085565; Le Lionnais 1983) is sometimes known as the first lemniscate constant, while

			(9)
			(10)

(OEIS A076390), where 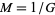 is the reciprocal of Gauss's constant, is sometimes known as the second lemniscate constant (Todd 1975, Gosper 1976, Lewanowicz and Paszowski 1995).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Finch, S. R. "Gauss' Lemniscate Constant." §6.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 420-423, 2003.

Gosper, R. W. "A Calculus of Series Rearrangements." In Algorithms and Complexity: New Directions and Recent Results. Proc. 1976 Carnegie-Mellon Conference (Ed. J. F. Traub). New York: Academic Press, pp. 121-151, 1976.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 37, 1983.

Levin, A. "A Geometric Interpretation of an Infinite Product for the Lemniscate Constants." Amer. Math. Monthly 113, 510-520, 2006.

Lewanowicz, S. and Paszowski, S. "An Analytic Method for Convergence Acceleration of Certain Hypergeometric Series." Math. Comput. 64, 691-713, 1995.

Sloane, N. J. A. Sequences A062539, A064853, A076390, and A085565 in "The On-Line Encyclopedia of Integer Sequences."

Todd, J. "The Lemniscate Constant." Comm. ACM 18, 14-19 and 462, 1975.