Champernowne's constant

(1)

(OEIS A033307) is the number obtained by concatenating the positive integers and interpreting them as decimal digits to the right of a decimal point. It is normal in base 10 (Champernowne 1933, Bailey and Crandall 2002). Mahler (1961) showed it to also be transcendental. The constant has been computed to  digits by E. W. Weisstein (Jul. 3, 2013) using the Wolfram Language.

The infinite sequence of digits in Champernowne's constant is sometimes known as Barbier's infinite word (Allouche and Shallit 2003, pp. 114, 299 and 334).

The number of digits after concatenation of the first, second, ... primes are given by 1, 2, 3, 4, 6, 8, 10, 12, 14, 16, ... (OEIS A068670).

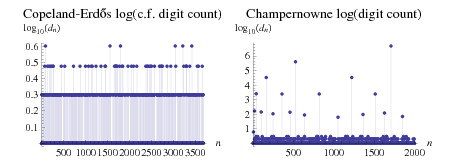
The Champernowne constant continued fraction contains sporadic very large terms, making the continued fraction difficult to calculate. However, the size of the continued fraction high-water marks display apparent patterns (Sikora 2012). Interestingly, the Copeland-Erdős constant, which is the decimal number obtained by concatenating the primes (instead of all the positive integers), has a well-behaved continued fraction that does not show the "large term" phenomenon.

The base- Champernowne constant is implemented in the Wolfram Language as ChampernowneNumber[b]. The base-2 and base-3 Champernowne constants are known as the binary and ternary Champernowne constants, respectively.

A nested sum for the -ary Champernowne constant is given by

(2)

An explicit formula for the -ary Champernowne constant is given by

(3)

where

			(4)
			(5)

(Parkin, pers. comm.). The analytic expression for the addend  in equation (3) is therefore

(6)

This allows convergents to the Champernowne constant  to be computed directly from the base  without explicit reference to the position of the terms.

REFERENCES:

Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 401 and 478, 2003.

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Champernowne, D. G. "The Construction of Decimals Normal in the Scale of Ten." J. London Math. Soc. 8, 1933.

Copeland, A. H. and Erdős, P. "Note on Normal Numbers." Bull. Amer. Math. Soc. 52, 857-860, 1946.

Finch, S. R. "Minkowski-Bower Constant." §6.9 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 441-443, 2003.

Mahler, K. Lectures on Diophantine Approximations, Part I: g-adic Numbers and Roth's Theorem. Notre Dame, Indiana: University of Notre Dame Press, 1961.

Niven, I. M. Irrational Numbers. New York: Wiley, p. 112, 1956.

Parkin, S. T. "An Identity for Champernowne's Constant." http://www.snorkey.com/math/Champ/champ.html.

Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, pp. 282-283, 2002.

 Rytin, M. "Champernowne Constant and Its Continued Fraction Expansion." http://library.wolfram.com/infocenter/MathSource/2876/.

Sikora, J. K. "On the High Water Mark Convergents of Champernowne's Constant in Base Ten." 3 Oct 2012. http://arxiv.org/abs/1210.1263.

Sloane, N. J. A. Sequences A030167 and A068670 in "The On-Line Encyclopedia of Integer Sequences."

Stoneham, R. "A General Arithmetic Construction of Transcendental Non-Liouville Normal Numbers from Rational Functions." Acta Arith. 16, 239-253, 1970.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 26, 1986.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.