A beautiful approximation to the Euler-Mascheroni constant 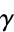 is given by

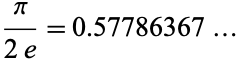(1)

(OEIS A086056; E. W. Weisstein, Apr. 18, 2006), which is good to three decimal digits.

In 1982-1983, Odena gave the strange approximation

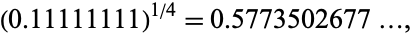(2)

which is effectively

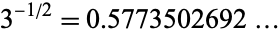(3)

(Munroe 2012).

Castellanos (1988) gave

			(4)
			(5)
			(6)
			(7)

which are good to 6, 8, 9, 14, and 14 digits, respectively.

An approximation involving unit fractions due to P. Galliani (pers. comm., April 1, 2002) is given by

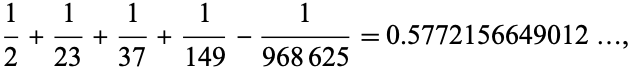(8)

which differs from 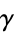 by 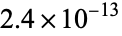, i.e., is good to 12 digits.

Ed Pegg, Jr. (pers. comm., March 2, 2002) found

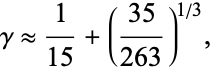(9)

which is good to 8 digits.

M. Hudson (pers. comm., Sept. 3, 2004) found the approximations

			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)

where 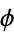 is the golden ratio, which are good to 5, 5, 6, 7, 7, 8, and 8 digits, respectively.

G. W. Barbosa (pers. comm., Mar. 26 and Apr. 2, 2007) gave

			(17)
			(18)
			(19)

which are good to 10 decimal digits, and where the second approximation is a difference of two pandigital parts. Barbosa (pers. comm., Jan. 7, 2008) also gave the pandigital approximation

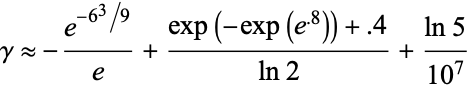(20)

which is good to 13 decimal digits.

REFERENCES:

Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.

Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.

Friedman, E. "Problem of the Month (August 2004)." http://www.stetson.edu/~efriedma/mathmagic/0804.html.

Munroe, R. "A Table of Slightly Wrong Equations and Identities Useful for Approximations and/or Trolling Teachers." xkcd: A Webcomic of Romance, Sarcasm, Math, and Language. http://xkcd.com/1047/. Apr. 2012.

Sloane, N. J. A. Sequences A086056 in "The On-Line Encyclopedia of Integer Sequences."