Bauer,s Identical Congruence
المؤلف:
Hardy, G. H. and Wright, E. M. J
المصدر:
London Math. Soc. 9
الجزء والصفحة:
...
2-1-2020
1655
Bauer's Identical Congruence
Let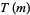 
denote the set of the 
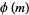numbers less than and relatively prime to 
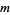, where 
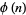is the totient function. Define
 |
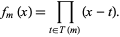(1)
|
Then a theorem of Lagrange states that
 |
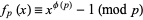(2)
|
for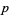 
an odd prime (Hardy and Wright 1979, p. 98). Actually, this relationship holds for some composite values as well. Value for which it holds are 
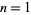, 3, 4, 5, 6, 7, 10, 11, 13, 17, 19, 23, 29, ... (OEIS A158008).
This can be generalized as follows. Let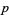 
be an odd prime divisor of 
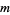and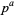 
the highest power which divides 
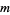, then
 |
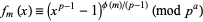(3)
|
and, in particular,
 |
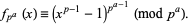(4)
|
Now, if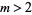 
is even and 
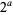is the highest power of 2 that divides 
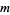, then
 |
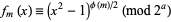(5)
|
and, in particular,
 |
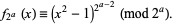(6)
|
REFERENCES:
Bauer. Nouvelles annales 2, 256-264, 1902.
Hardy, G. H. and Wright, E. M. J. London Math. Soc. 9, 38-41 and 240, 1934.
Hardy, G. H. and Wright, E. M. "Bauer's Identical Congruence." §8.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 98-100, 1979.
Sloane, N. J. A. Sequence A158008 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
