
Full Reptend Prime
 المؤلف:
Conway, J. H. and Guy, R. K.
المؤلف:
Conway, J. H. and Guy, R. K.
 المصدر:
The Book of Numbers. New York: Springer-Verlag, 1996.
المصدر:
The Book of Numbers. New York: Springer-Verlag, 1996.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 24-11-2019
24-11-2019
 1019
1019
Full Reptend Prime
A prime 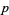 for which
for which 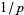 has a maximal period decimal expansion of
has a maximal period decimal expansion of 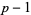 digits. Full reptend primes are sometimes also called long primes (Conway and Guy 1996, pp. 157-163 and 166-171). There is a surprising connection between full reptend primes and Fermat primes.
digits. Full reptend primes are sometimes also called long primes (Conway and Guy 1996, pp. 157-163 and 166-171). There is a surprising connection between full reptend primes and Fermat primes.
A prime 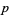 is full reptend iff 10 is a primitive root modulo
is full reptend iff 10 is a primitive root modulo 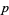 , which means that
, which means that
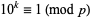 |
(1)
|
for 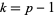 and no
and no 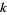 less than this. In other words, the multiplicative order of
less than this. In other words, the multiplicative order of 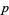 (mod 10) is
(mod 10) is 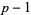 . For example, 7 is a full reptend prime since
. For example, 7 is a full reptend prime since 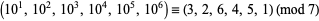 .
.
The full reptend primes are 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, ... (OEIS A001913). The first few decimal expansions of these are
Here, the numbers 142857, 5882352941176470, 526315789473684210, ... (OEIS A004042) corresponding to the periodic parts of these decimal expansions are called cyclic numbers. No general method is known for finding full reptend primes.
The number of full reptend primes less than 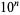 for
for 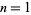 , 2, ... are 1, 9, 60, 467, 3617, ... (OEIS A086018).
, 2, ... are 1, 9, 60, 467, 3617, ... (OEIS A086018).
A necessary (but not sufficient) condition that 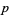 be a full reptend prime is that the number
be a full reptend prime is that the number 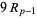 (where
(where 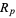 is a repunit) is divisible by
is a repunit) is divisible by 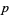 , which is equivalent to
, which is equivalent to 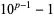 being divisible by
being divisible by 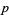 . For example, values of
. For example, values of 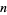 such that
such that 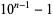 is divisible by
is divisible by 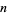 are given by 1, 3, 7, 9, 11, 13, 17, 19, 23, 29, 31, 33, 37, ... (OEIS A104381).
are given by 1, 3, 7, 9, 11, 13, 17, 19, 23, 29, 31, 33, 37, ... (OEIS A104381).
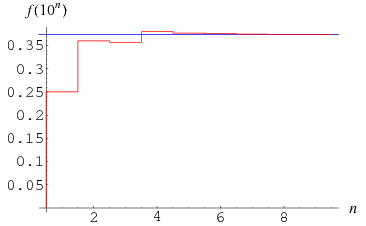
Artin conjectured that Artin's constant 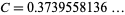 (OEIS A005596) is the fraction of primes
(OEIS A005596) is the fraction of primes 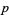 for which
for which 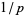 has decimal maximal period (Conway and Guy 1996). The first few fractions include primes up to
has decimal maximal period (Conway and Guy 1996). The first few fractions include primes up to 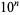 for
for 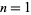 , 2, ... are 1/4, 9/25, 5/14, 467/1229, 3617/9592, 14750/39249, ... (OEIS A103362 and A103363), illustrated above together with the value of
, 2, ... are 1/4, 9/25, 5/14, 467/1229, 3617/9592, 14750/39249, ... (OEIS A103362 and A103363), illustrated above together with the value of 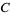 . D. Lehmer has generalized this conjecture to other bases, obtaining values that are small rational multiples of
. D. Lehmer has generalized this conjecture to other bases, obtaining values that are small rational multiples of  .
.
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, 1996.
Sloane, N. J. A. Sequences A001913/M4353, A004042, A005596, A006883/M1745, A086018, A103362, A103363, and A104381 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 71, 1986.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


