"Casting out nines" is an elementary check of a multiplication which makes use of the congruence 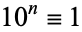 (mod 9). Let decimal numbers be written 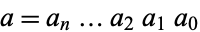, , 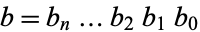and their product be 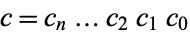. Let the sums of the digits of these numbers be 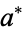, , 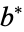and 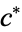. Then 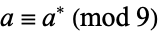, , 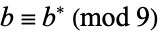and 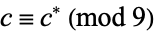. Furthermore 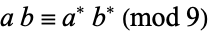, so 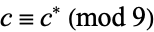. So if  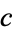and 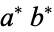 are incongruent (mod 9), the multiplication has been done incorrectly.

For example, 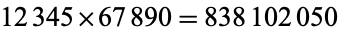. The sum-of-digits of 12345 and 67890 are 15 and 30, respectively, and the product of these is 450. Similarly, the sum-of-digits of 838102050 is 27. And 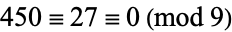, so the check shows agreement.

Casting out nines is also an addition test, since 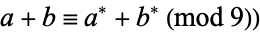, and a subtraction test, since 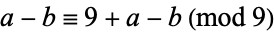. It can also be used as a division test for  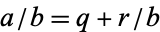(i.e.,  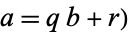since .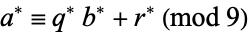

Casting out nines was transmitted to Europe by the Arabs, but was probably developed somewhere on the Indian subcontinent and is therefore sometimes also called "the Hindu check," with "Hindu" simply meaning the people of the Indian subcontinent.

The procedure was described by Fibonacci in his Liber Abaci (Wells 1986, p. 74).

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 28-29, 1996.

Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, p. 115, 2000.

Hilton, P.; Holton, D.; and Pedersen, J. "Casting Out 9's and 11's: Tricks of the Trade." Mathematical Reflections in a Room with Many Mirrors. New York: Springer-Verlag, pp. 53-57, 1997.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 74, 1986.