
Symmetric Polynomial
 المؤلف:
Borwein, P. and Erdélyi, T
المؤلف:
Borwein, P. and Erdélyi, T
 المصدر:
Polynomials and Polynomial Inequalities. New York: Springer-Verlag
المصدر:
Polynomials and Polynomial Inequalities. New York: Springer-Verlag
 الجزء والصفحة:
...
الجزء والصفحة:
...
 23-2-2019
23-2-2019
 1401
1401
Symmetric Polynomial
A symmetric polynomial on  variables
variables  , ...,
, ...,  (also called a totally symmetric polynomial) is a function that is unchanged by any permutation of its variables. In other words, the symmetric polynomials satisfy
(also called a totally symmetric polynomial) is a function that is unchanged by any permutation of its variables. In other words, the symmetric polynomials satisfy
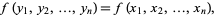 |
(1)
|
where 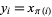 and
and 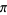 being an arbitrary permutation of the indices 1, 2, ...,
being an arbitrary permutation of the indices 1, 2, ..., 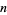 .
.
For fixed 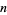 , the set of all symmetric polynomials in
, the set of all symmetric polynomials in 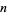 variables forms an algebra of dimension
variables forms an algebra of dimension 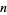 . The coefficients of a univariate polynomial
. The coefficients of a univariate polynomial 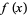 of degree
of degree 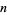 are algebraically independent symmetric polynomials in the roots of
are algebraically independent symmetric polynomials in the roots of 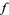 , and thus form a basis for the set of all such symmetric polynomials.
, and thus form a basis for the set of all such symmetric polynomials.
There are four common homogeneous bases for the symmetric polynomials, each of which is indexed by a partition 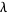 (Dumitriu et al. 2004). Letting
(Dumitriu et al. 2004). Letting 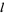 be the length of
be the length of 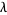 , the elementary functions
, the elementary functions 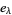 , complete homogeneous functions
, complete homogeneous functions 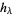 , and power-sum functions
, and power-sum functions 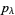 are defined for
are defined for 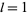 by
by
and for 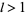 by
by
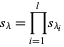 |
(5)
|
where 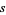 is one of
is one of 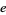 ,
, 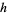 or
or 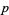 . In addition, the monomial functions
. In addition, the monomial functions 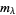 are defined as
are defined as
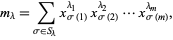 |
(6)
|
where 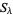 is the set of permutations giving distinct terms in the sum and
is the set of permutations giving distinct terms in the sum and 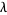 is considered to be infinite.
is considered to be infinite.
As several different abbreviations and conventions are in common use, care must be taken when determining which symmetric polynomial is in use.
The elementary symmetric polynomials 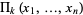 (sometimes denoted
(sometimes denoted 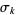 or
or 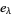 ) on
) on 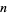 variables
variables ![<span style=]() {x_1,...,x_n}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline41.gif" style="height:14px; width:66px" /> are defined by
{x_1,...,x_n}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline41.gif" style="height:14px; width:66px" /> are defined by
The 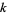 th elementary symmetric polynomial is implemented in the Wolfram Language as SymmetricPolynomial[k,
th elementary symmetric polynomial is implemented in the Wolfram Language as SymmetricPolynomial[k, ![<span style=]() {" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline61.gif" style="height:14px; width:5px" />x1, ..., xn
{" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline61.gif" style="height:14px; width:5px" />x1, ..., xn![<span style=]() }" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline62.gif" style="height:14px; width:5px" />]. SymmetricReduction[f,
}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline62.gif" style="height:14px; width:5px" />]. SymmetricReduction[f, ![<span style=]() {" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline63.gif" style="height:14px; width:5px" />x1, ..., xn
{" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline63.gif" style="height:14px; width:5px" />x1, ..., xn![<span style=]() }" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline64.gif" style="height:14px; width:5px" />] gives a pair of polynomials
}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline64.gif" style="height:14px; width:5px" />] gives a pair of polynomials ![<span style=]() {p,q}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline65.gif" style="height:14px; width:33px" /> in
{p,q}" src="http://mathworld.wolfram.com/images/equations/SymmetricPolynomial/Inline65.gif" style="height:14px; width:33px" /> in 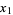 , ...,
, ..., 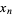 where
where 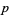 is the symmetric part and
is the symmetric part and 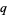 is the remainder.
is the remainder.
Alternatively, 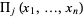 can be defined as the coefficient of
can be defined as the coefficient of 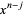 in the generating function
in the generating function
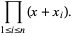 |
(13)
|
For example, on four variables 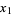 , ...,
, ..., 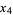 , the elementary symmetric polynomials are
, the elementary symmetric polynomials are
The power sum 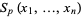 is defined by
is defined by
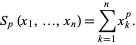 |
(18)
|
The relationship between 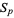 and
and 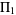 , ...,
, ..., 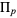 is given by the so-called Newton-Girard formulas. The related function
is given by the so-called Newton-Girard formulas. The related function 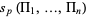 with arguments given by the elementary symmetric polynomials (not
with arguments given by the elementary symmetric polynomials (not 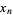 ) is defined by
) is defined by
It turns out that 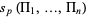 is given by the coefficients of the generating function
is given by the coefficients of the generating function
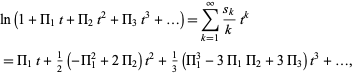 |
(21)
|
so the first few values are
In general, 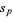 can be computed from the determinant
can be computed from the determinant
 |
(26)
|
(Littlewood 1958, Cadogan 1971). In particular,
(Schroeppel 1972), as can be verified by plugging in and multiplying through.
REFERENCES:
Borwein, P. and Erdélyi, T. Polynomials and Polynomial Inequalities. New York: Springer-Verlag, p. 5, 1995.
Cadogan, C. C. "The Möbius Function and Connected Graphs." J. Combin. Th. B 11, 193-200, 1971.
Dumitriu, I.; Edelman, A.; and Shuman, G. "MOPS: Multivariate Orthogonal Polynomials (Symbolically)." Preprint. March 26, 2004.
Littlewood, J. E. A University Algebra, 2nd ed. London: Heinemann, 1958.
Schroeppel, R. Item 6 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 4, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/geometry.html#item6.
Séroul, R. "Newton-Girard Formulas." §10.12 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 278-279, 2000.
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


