Second-Order Ordinary Differential Equation Second Solution
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
5-7-2018
1466
Second-Order Ordinary Differential Equation Second Solution
If one solution (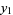
) to a second-order ordinary differential equation
 |
(1)
|
is known, the other (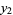
) may be found using the so-called reduction of order method. From Abel's differential equation identity
 |
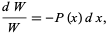(2)
|
where
 |
(3)
|
is the Wronskian.
Integrating gives
 |
(4)
|
 |
(5)
|
and solving for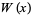 
gives
 |
(6)
|
But
 |
(7)
|
so combining (◇) and (◇) yields
 |
(8)
|
 |
(9)
|
Disregarding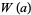 
, since it is simply a multiplicative constant, and the constants 
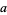and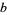 
, which will contribute a solution which is not linearly independent of 
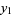, leaves
 |
(10)
|
In the special case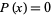 
, this simplifies to
 |
(11)
|
If both general solutions to a second-order nonhomogeneous differential equation are known, variation of parameters can be used to find the particular solution.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
