The Laguerre differential equation is given by

(1)

Equation (1) is a special case of the more general associated Laguerre differential equation, defined by

(2)

where 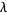 and  are real numbers (Iyanaga and Kawada 1980, p. 1481; Zwillinger 1997, p. 124) with .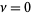

The general solution to the associated equation (2) is

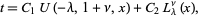(3)

where 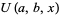 is a confluent hypergeometric function of the first kind and  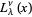is a generalized Laguerre polynomial.

Note that in the special case 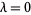, the associated Laguerre differential equation is of the form

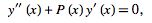(4)

so the solution can be found using an integrating factor

			(5)
			(6)
			(7)
			(8)

as

			(9)
			(10)
			(11)

where 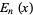 is the En-function.

The associated Laguerre differential equation has a regular singular point at 0 and an irregular singularity at 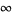. It can be solved using a series expansion,

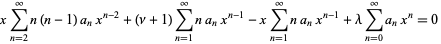	(12)
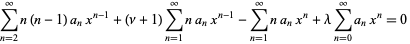	(13)
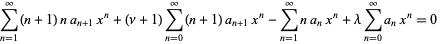	(14)
{[(n+1)n+(nu+1)(n+1)]a_(n+1)-na_n+lambdaa_n}x^n=0 " src="http://mathworld.wolfram.com/images/equations/LaguerreDifferentialEquation/Inline33.gif" style="height:44px; width:441px" />	(15)
	(16)

This requires

			(17)
			(18)

for 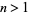. Therefore,

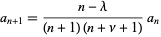(19)

for 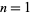, 2, ..., so

			(20)
			(21)
			(22)

If 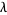 is a nonnegative integer, then the series terminates and the solution is given by

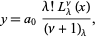(23)

where 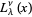 is an associated Laguerre polynomial and  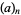is a Pochhammer symbol. In the special case 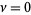, the associated Laguerre polynomial collapses to a usual Laguerre polynomial and the solution collapses to

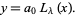(24)

REFERENCES:

Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1481, 1980.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 120, 1997.