Chebyshev Differential Equation
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
11-6-2018
1588
Chebyshev Differential Equation
 |
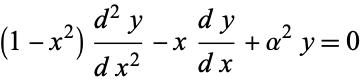(1)
|
for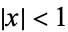 
. The Chebyshev differential equation has regular singular points at 
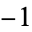, 1, and 
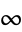. It can be solved by series solution using the expansions
Now, plug equations (6) and (8) into the original equation (◇) to obtain
 |
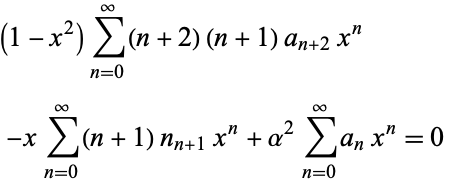(9)
|
 |
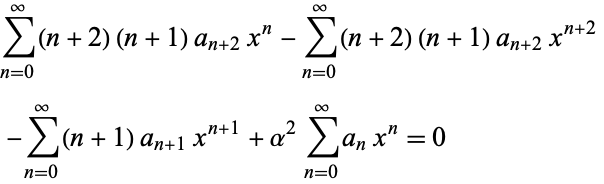(10)
|
 |
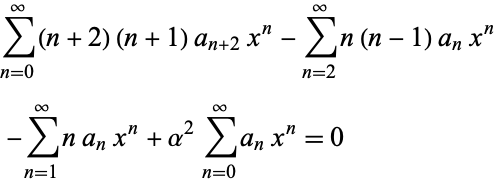(11)
|
![2·1a_2+3·2a_3x-1·ax+alpha^2a_0+alpha^2a_1x
+sum_(n=2)^infty[(n+2)(n+1)a_(n+2)-n(n-1)a_n-na_n+alpha^2a_n]x^n=0](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation5.gif) |
(12)
|
![(2a_2+alpha^2a_0)+[(alpha^2-1)a_1+6a_3]x
+sum_(n=2)^infty[(n+2)(n+1)a_(n+2)+(alpha^2-n^2)a_n]x^n=0,](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation6.gif) |
(13)
|
so
 |
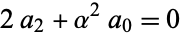(14)
|
 |
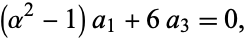(15)
|
and by induction,
 |
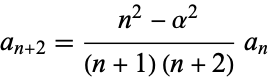(16)
|
for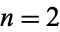 
, 3, ....
Since (14) and (15) are special cases of (16), the general recurrence relation can be written
 |
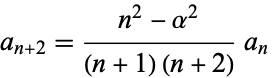(17)
|
for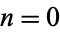 
, 1, .... From this, we obtain for the even coefficients
and for the odd coefficients
The even coefficients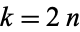 
can be given in closed form as
and the odd coefficient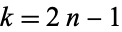s 
as
The general solution is then given by summing over all indices,
![y=a_0[1+sum_(k=2,4,...)^infty(a_(k even))/(k!)x^k]
+[x+sum_(k=3,5,...)^infty(a_(k odd))/(k!)x^k],](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation11.gif) |
(28)
|
which can be done in closed form as
 |
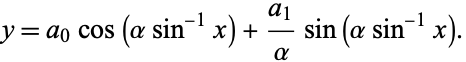(29)
|
Performing a change of variables gives the equivalent form of the solution
where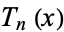 
is a Chebyshev polynomial of the first kind and 
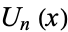is a Chebyshev polynomial of the second kind. Another equivalent form of the solution is given by
![y=c_1cosh[alphaln(x+sqrt(x^2-1))]
+ic_2sinh[alphaln(x+sqrt(x^2-1))].](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation13.gif) |
(32
|
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 735, 1985.
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, pp. 232 and 252, 1986.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
