


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-03-18
التاريخ: 2023-03-30
التاريخ: 8-1-2021
التاريخ: 23-1-2021
|
Notice that in the above process we have obtained something very interesting. For we have not only a number for the index of refraction which can be computed from the basic atomic quantities, but we have also learned how the index of refraction should vary with the frequency ω of the light. This is something we would never understand from the simple statement that “light travels slower in a transparent material.” We still have the problem, of course, of knowing how many atoms per unit volume there are, and what is their natural frequency ω0. We do not know this just yet, because it is different for every different material, and we cannot get a general theory of that now. Formulation of a general theory of the properties of different substances—their natural frequencies, and so on—is possible only with quantum atomic mechanics. Also, different materials have different properties and different indexes, so we cannot expect, anyway, to get a general formula for the index which will apply to all substances.
However, we shall discuss the formula we have obtained, in various possible circumstances. First of all, for most ordinary gases (for instance, for air, most colorless gases, hydrogen, helium, and so on) the natural frequencies of the electron oscillators correspond to ultraviolet light. These frequencies are higher than the frequencies of visible light, that is, ω0 is much larger than ω of visible light, and to a first approximation, we can disregard ω2 in comparison with ω20. Then we find that the index is nearly constant. So, for a gas, the index is nearly constant. This is also true for most other transparent substances, like glass. If we look at our expression a little more closely, however, we notice that as ω rises, taking a little bit more away from the denominator, the index also rises. So, n rises slowly with frequency. The index is higher for blue light than for red light. That is the reason why a prism bends the light more in the blue than in the red.
The phenomenon that the index depends upon the frequency is called the phenomenon of dispersion, because it is the basis of the fact that light is “dispersed” by a prism into a spectrum. The equation for the index of refraction as a function of frequency is called a dispersion equation. So, we have obtained a dispersion equation. (In the past few years “dispersion equations” have been finding a new use in the theory of elementary particles.)
Our dispersion equation suggests other interesting effects. If we have a natural frequency ω0 which lies in the visible region, or if we measure the index of refraction of a material like glass in the ultraviolet, where ω gets near ω0, we see that at frequencies very close to the natural frequency the index can get enormously large, because the denominator can go to zero. Next, suppose that ω is greater than ω0. This would occur, for example, if we take a material like glass, say, and shine x-ray radiation on it. In fact, since many materials which are opaque to visible light, like graphite for instance, are transparent to x-rays, we can also talk about the index of refraction of carbon for x-rays. All the natural frequencies of the carbon atoms would be much lower than the frequency we are using in the x-rays, since x-ray radiation has a very high frequency. The index of refraction is that given by our dispersion equation if we set ω0 equal to zero (we neglect ω20 in comparison with ω2).
A similar situation would occur if we beam radio waves (or light) on a gas of free electrons. In the upper atmosphere electrons are liberated from their atoms by ultraviolet light from the sun and they sit up there as free electrons. For free electrons ω0=0 (there is no elastic restoring force). Setting ω0=0 in our dispersion equation yields the correct formula for the index of refraction for radiowaves in the stratosphere, where N is now to represent the density of free electrons (number per unit volume) in the stratosphere. But let us look again at the equation, if we beam x-rays on matter, or radiowaves (or any electric waves) on free electrons the term (ω20−ω2) becomes negative, and we obtain the result that n is less than one. That means that the effective speed of the waves in the substance is faster than c! Can that be correct?
It is correct. In spite of the fact that it is said that you cannot send signals any faster than the speed of light, it is nevertheless true that the index of refraction of materials at a particular frequency can be either greater or less than 1. This just means that the phase shift which is produced by the scattered light can be either positive or negative. It can be shown, however, that the speed at which you can send a signal is not determined by the index at one frequency, but depends on what the index is at many frequencies. What the index tells us is the speed at which the nodes (or crests) of the wave travel. The node of a wave is not a signal by itself. In a perfect wave, which has no modulations of any kind, i.e., which is a steady oscillation, you cannot really say when it “starts,” so you cannot use it for a timing signal. In order to send a signal, you have to change the wave somehow, make a notch in it, make it a little bit fatter or thinner. That means that you have to have more than one frequency in the wave, and it can be shown that the speed at which signals travel is not dependent upon the index alone, but upon the way that the index changes with the frequency. Then we will calculate for you the actual speed of signals through such a piece of glass, and you will see that it will not be faster than the speed of light, although the nodes, which are mathematical points, do travel faster than the speed of light.
Just to give a slight hint as to how that happens, you will note that the real difficulty has to do with the fact that the responses of the charges are opposite to the field, i.e., the sign has gotten reversed. Thus, in our expression for x (Eq. 31.16) the displacement of the charge is in the direction opposite to the driving field, because (ω20−ω2) is negative for small ω0. The formula says that when the electric field is pulling in one direction, the charge is moving in the opposite direction.
How does the charge happen to be going in the opposite direction? It certainly does not start off in the opposite direction when the field is first turned on. When the motion first starts there is a transient, which settles down after a while, and only then is the phase of the oscillation of the charge opposite to the driving field. And it is then that the phase of the transmitted field can appear to be advanced with respect to the source wave. It is this advance in phase which is meant when we say that the “phase velocity” or velocity of the nodes is greater than c. In Fig. 31–4 we give a schematic idea of how the waves might look for a case where the wave is suddenly turned on (to make a signal). You will see from the diagram that the signal (i.e., the start of the wave) is not earlier for the wave which ends up with an advance in phase.
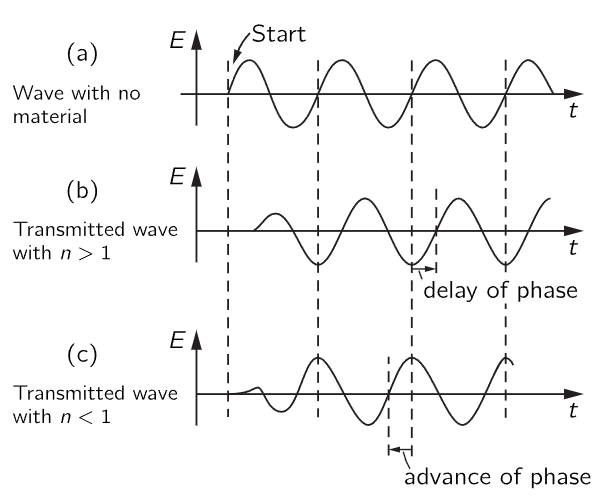
Fig. 31–4. Wave “signals.”
Let us now look again at our dispersion equation. We should remark that our analysis of the refractive index gives a result that is somewhat simpler than you would actually find in nature. To be completely accurate we must add some refinements. First, we should expect that our model of the atomic oscillator should have some damping force (otherwise once started it would oscillate forever, and we do not expect that to happen). We have worked out before (Eq. 23.8) the motion of a damped oscillator and the result is that the denominator in Eq. (31.16), and therefore in (31.19), is changed from (ω20−ω2) to (ω20−ω2+iγω), where γ is the damping coefficient.
We need a second modification to take into account the fact that there are several resonant frequencies for a particular kind of atom. It is easy to fix up our dispersion equation by imagining that there are several different kinds of oscillators, but that each oscillator acts separately, and so we simply add the contributions of all the oscillators. Let us say that there are Nk electrons per unit of volume, whose natural frequency is ωk and whose damping factor is γk. We would then have for our dispersion equation
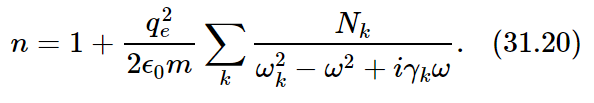
We have, finally, a complete expression which describes the index of refraction that is observed for many substances.1 The real part of the index described by this formula varies with frequency roughly like the curve shown in Fig. 31–5(a).
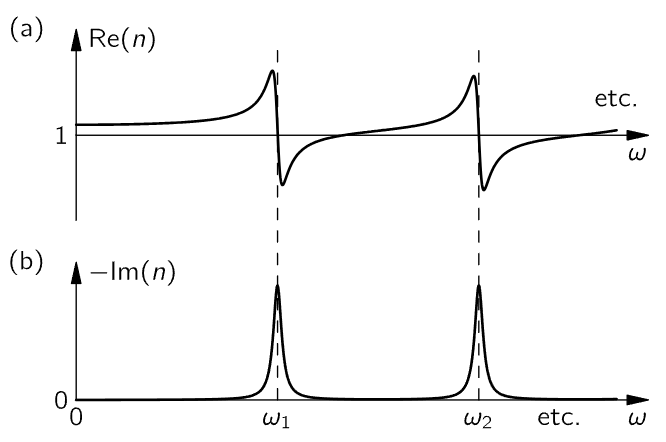
Fig. 31–5. The index of refraction as a function of frequency.
You will note that so long as ω is not too close to one of the resonant frequencies, the slope of the curve is positive. Such a positive slope is called “normal” dispersion (because it is clearly the most common occurrence). Very near the resonant frequencies, however, there is a small range of ω’s for which the slope is negative. Such a negative slope is often referred to as “anomalous” (meaning abnormal) dispersion, because it seemed unusual when it was first observed, long before anyone even knew there were such things as electrons. From our point of view both slopes are quite “normal”!
_______________________________________________________
Margin
1- Actually, although in quantum mechanics Eq. (31.20) is still valid, its interpretation is somewhat different. In quantum mechanics even an atom with one electron, like hydrogen, has several resonant frequencies. Therefore, Nk is not really the number of electrons having the frequency ωk, but is replaced instead by Nfk, where N is the number of atoms per unit volume and fk (called the oscillator strength) is a factor that tells how strongly the atom exhibits each of its resonant frequencies ωk.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|