المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Laplace-Mehler Integral |
 1329
 05:11 مساءً
date: 21-8-2018 |
Author : Hobson, E. W. 
Book or Source : The Theory of Spherical and Ellipsoidal Harmonics. New York: Chelsea, 1955. 
Page and Part : ...|
Read More
Date: 2-5-2019
1732
Date: 30-3-2019
2109
Date: 28-8-2019
1707
|
The Lehmer-Mahler is the following integral representation for the Legendre polynomial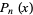 
:
 |
 |
 |
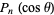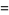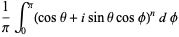(1) |
 |
 |
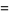![(sqrt(2))/piint_0^theta(cos[(n+1/2)phi])/(sqrt(cosphi-costheta))dphi](http://mathworld.wolfram.com/images/equations/Laplace-MehlerIntegral/Inline7.gif) |
(2) |
 |
 |
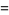![(sqrt(2))/piint_theta^pi(sin[(n+1/2)phi])/(sqrt(costheta-cosphi))dphi.](http://mathworld.wolfram.com/images/equations/Laplace-MehlerIntegral/Inline10.gif) |
(3) |
REFERENCES:
Hobson, E. W. The Theory of Spherical and Ellipsoidal Harmonics. New York: Chelsea, 1955.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1463, 1980.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
