مقاييس النزعة المركزية  Central Tendency  :

في كثير من النواحي التطبيقية يكون الباحث في حاجة الى حساب بعض المؤشرات التي يمكن الاعتماد عليها في وصف الظاهرة من حيث القيمة التي تتوسط القيم ، ومن حيث التعرف على مدى تجانس القيم التي يأخذها المتغير، وايضاً ما اذا كان هناك قيم شاذة او لا .

والاعتماد على العرض البياني وحده لا يكفي ، لذا يتناول هذا الفصل والذي يليه عرض بعض المقاييس الاحصائية والتي يمكن من خلالها التعرف على خصائص الظاهرة محل البحث  وكذلك امكانية مقارنة ظاهرتين او اكثر، ومن اهم هذه المقاييس مقاييس النزعة المركزية والتشتت . 

تسمى مقاييس النزعة المركزية بمقاييس الموضع او المتوسطات ، وهي  القيم التي تتركز القيم حولها ، ومن هذه المقاييس ؛ الوسط الحسابي ، المنوال ، الوسيط ، الوسط الهندسي ، والوسط التوافقي ، الرباعيات ، وفيما يلي عرض لأهم هذه المقاييس .

الوسط الحسابي   Arithmetic mean  : من أهم مقاييس الترعة المركزية ، وأكثرها استخداما في النواحي التطبيقية ، ويمكن حسابه للبيانات المبوبة وغير المبوبة ، كما يلي :

أولا: الوسط الحسابي للبيانات غير المبوبة: يعرف الوسط الحسابي بشكل عام على أنه مجموع القيم مقسوما على عددها . فإذا كان لدينا n من القيم ، ويرمز لها بالرمز 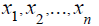 فإن الوسط الحسابي لهذه القيم ، ونرمز له بالرمز 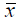يحسب بالمعادلة التالية :

حيث يدل الرمز 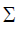 على المجموع .

مثال(3-1)فيما يلي درجات8 طلاب في مقرر122إحصاء تطبيقي 40، 36، 40، 35، 37، 42، 32، 34 .

والمطلوب إيجاد الوسط الحسابي لدرجة الطالب في الامتحان .

الحل لإيجاد الوسط الحسابي للدرجات تطبق المعادلة السابقة كما يلي:

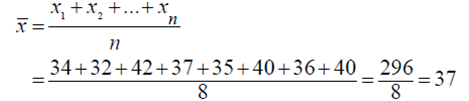
أي أن الوسط الحسابي لدرجة الطالب في اختبار مقرر122 إحصاء يساوي 37 درجة.

ثانيا: الوسط الحسابي للبيانات المبوبة: من المعلوم أن القيم الأصلية ، لا يمكن معرفتها من جدول التوزيع التكراري ، حيث أن هذه القيم موضوعة في شكل فئات ، ولذا يتم التعبير عن كل قيمة من القيم التي تقع داخل حدود الفئة بمركز هذه الفئة ، ومن ثم يؤخذ في الاعتبار أن مركز الفئة هو القيمة التقديرية لكل مفردة تقع في هذه الفئة.

فإذا كانت k هي عدد الفئات ، وكانت 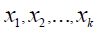 هي مراكز هذه الفئات،  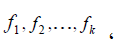هي التكرارات ، فإن الوسط الحسابي يحسب بالمعادلة التالية:

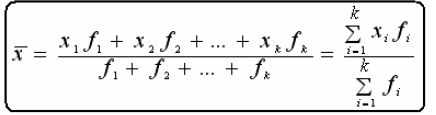
مثال ( 3-2) الجدول التالي يعرض توزيع 40 تلميذ حسب أوزانهم.

والمطلوب إيجاد الوسط الحسابي.

الحل: لحساب الوسط الحسابي باستخدام المعادلة السابقة يتم إتباع الخطوات التالية :

1- إيجاد مجموع التكرارات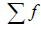

2- حساب مراكز الفئات x

3- ضرب مركز الفئة في التكرار المناظر له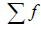 وحساب المجموع 

4- حساب الوسط الحسابي بتطبيق المعادلة.

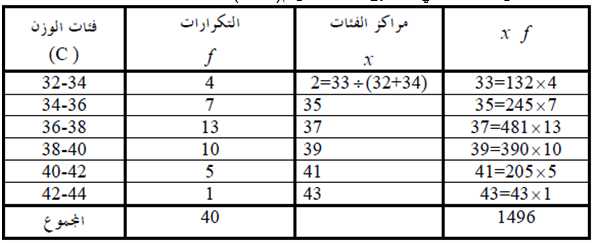
إذا الوسط الحسابي لوزن التلميذ هو :

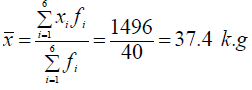
أي أن متوسط وزن التلميذ يساوي 37.4kg

خصائص الوسط الحسابي: يتصف الوسط الحسابي بعدد من الخصائص ، ومن هذه الخصائص ما يلي :

1- الوسط الحسابي للمقدار الثابت يساوى الثابت نفسه ، أي أنه إذا كانت قيم x هي 

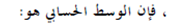
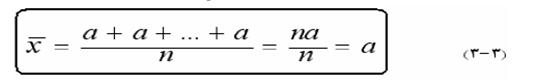
ومثال على ذلك ، لو اخترنا مجموعة من 5 طلاب ، ووجدنا أن كل طالب وزنه 63 كيلوجرام فإن متوسط وزن الطالب في هذه المجموعة هو :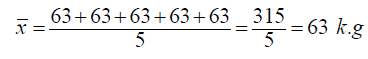 

2- مجموع انحرافات القيم عن وسطها الحسابي يساوى صفرا ، ويعبر عن هذه الخاصية بالمعادلة:

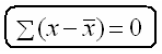
ويمكن التحقق من هذه الخاصية باستخدام بيانات مثال ( 3-1) نجد أن درجات الطلاب هي :

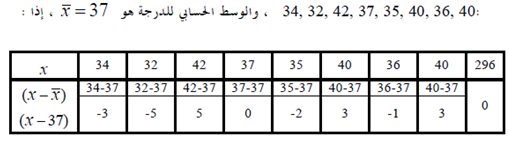
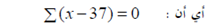
3- إذا أضيف مقدار ثابت إلى كل قيمة من القيم ، فإن الوسط الحسابي للقيم المعدلة (بعد الإضافة) يساوى الوسط الحسابي للقيم الأصلية (قبل الإضافة) مضافا إليها هذا المقدار الثابت .

فإذا كانت القيم هي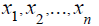  وتم إضافة مقدار ثابت (a) إلى كل قيمة من القيم ، ونرمز للقيم الجديدة بالرمز y       

       حيث أن 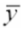  هو الوسط الحسابي للقيم الجديدة ، ويمكن التحقق من هذه الخاصية باستخدام بيانات مثال رقم ( 3-1)
إذا قرر المصحح إضافة 5 درجات لكل طالب ، فإن الوسط الحسابي للدرجات المعدلة يصبح قيمته 42=(5+37) ، والجدول التالي يبين ذلك .

4- إذا ضرب مقدار ثابت(a) في كل قيمة من القيم ، فإن الوسط الحسابي للقيم المعدلة (القيم الناتجة بعد الضرب) يساوي الوسط الحسابي للقيم الأصلية (القيم بعد التعديل) مضروبا في هذا المقدار الثابت .

أي أنه إذا كان y = a x ويكون الوسط الحسابي للقيم الجديدة y هو :

5- مجموع مربعات انحرافات القيم عن وسطها الحسابي أقل ما يمكن ، أي أن:

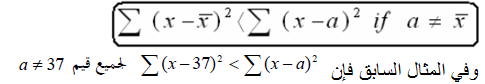
ثالثا: الوسط الحسابي المرجح: في بعض الأحيان يكون لكل قيمة من قيم المتغير أهمية نسبية تسمى أوزن ، أو ترجيحات ،وعدم أخذ هذه الأوزان في الاعتبار عند حساب الوسط الحسابي ، تكون القيمة المعبرة عن الوسط الحسابي غير دقيقة ، فمثلا لو أخذنا خمسة طلاب ، وسجلنا درجات هؤلاء الطلاب في مقرر الإحصاء التطبيقي ، وعدد ساعات الاستذكار في الأسبوع

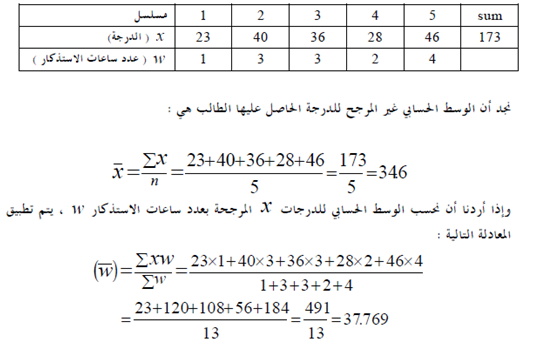
مزايا وعيوب الوسط الحسابي :

 يتميز الوسط الحسابي بالمزايا التالية :

 ــ أنه سهل الحساب . ·

 ــ يأخذ في الاعتبار كل القيم . ·

 ــ أنه أكثر المقاييس استخداما وفهما . ·

ومن عيوبه :

 ــ أنه يتأثر بالقيم الشاذة والمتطرفة . ·

 ــ يصعب حسابه في حالة البيانات الوصفية . ·

 ــ يصعب حسابه في حالة الجداول التكرارية المفتوحة .